Coursera의 Machine Learning Specialization강의를 정리한 내용입니다
Neural Network Training
TensorFlow implementation

왼쪽과 같은 neural network architecture를 사용한다면, 코드에서 neural network는 어떻게 훈련시킬 수 있을까?
첫번째 단계는 지난 강의에서 배웠던 것과 매우 비슷하다.
unit과 sigmoid activation function을 인자로 갖는 각 `Dense(layer)`를 `Sequential`로 묶어 하나의 model을 만들었다.
이후, 두번째 단계는 사용하려는 Tensorflow에 model 컴파일을 요청하는 것이다.
컴파일 단계에서 중요한 것은 loss가 무엇인지 지정해야 한다는 점이다..
이 경우에는 `BinaryCrossentropy()`함수를 loss로 사용한다.
loss function을 지정한 후 세 번째 단계는 2단계에서 지정한 loss function을 사용하여 1단계에서 지정한 model을 dataset X,Y에 맞추도록 Tensorflow에 지시해야한다는 점이다.
`model.fit`을 이용해 model을 fitting하는 과정을 수행하는데, 여기서 `epochs`는 기술적인 용어로 gradient descent와 같은 학습 알고리즘을 실행할 단계 수를 나타낸다.
Training Details
neural network를 자세하게 알아보기 전에, 먼저 logistic regression model을 어떻게 훈련했는지 생각해보자.

logistic regression model의 구축 1단계는 model을 정의하는 것이었다.
(input x와 parameter를 이용해서 output을 어떻게 산출하는지 계산하는 것)
코드상으론 오른쪽과 같이 `np.dot()`을 이용하여 dot product를 계산했으며, `np.exp()`를 이용해서 e의 지수승을 표현할 수 있었다.
2단계는 loss와 cost를 지정하는 것이었다.
코드 상으로 나타난 것은 logistic regression의 loss였음을 확인할 수 있다.
loss - single training example에서 계산
cost - 전체 training example의 loss를 평균낸 것
마지막 3단계는 gradient descent 알고리즘을 이용하여 cost function J를 최소화하기 위해 w와 b를 update하는 것이었다.
Tensorflow에서 neural network를 훈련 시키는 방법 또한 3단계로 동일하다.

1단계: `Sequential()` 함수를 이용해 input x와 parameter w,b를 어떻게 처리할 것인지에 대한 model을 구축한다.
2단계 : model을 컴파일하고 사용할 loss를 지정하는 것. loss 지정 후 전체 training example에 대해 평균을 구하면 Cost도 나온다.->loss로 `BinaryCrossentropy()`를 사용했다.
3단계 : neural network parameter를 update하여 cost function를 최소화한다.
-> `fit()` function으로 이를 수행할 수 있다. epochs는 learning algorithm을 작동시킬 횟수를 말했었다.
이 3단계를 더 자세하게 살펴보자.
1. Create the model

먼저, input x와 parameter w,b가 주어지면 출력값을 계산하는 방법을 지정해야한다.
(위의 code snippet은 neural network의 architecture를 지정하며 layer의 unit 개수, activation function, parameter에 대한 정보를 모두 담고있다.)
2. Loss and cost functions
두번째 단계에서는 loss function이 무엇인지 정의해야하며, loss function을 정의함으로써 cost function도 정의할 수 있다.

지금까지 흔히 쓰였던 손글씨 숫자 classification 문제에서 사용한 함수는 logistic regression에서 사용한 것과 동일하다. Tensorflow에서는 logistic regression의 loss를 binary cross entropy라고 부른다.
이름의 유래는 통계학에서 왔다. 통계학에서는 해당 함수를 cross entropy라고만 부른다. binary라는 것은 2진 문제라는 것을 강조하기 위해 추가적으로 붙인 것 뿐이다.
이후 이 loss를 사용하여 neural network를 컴파일 하도록 요청해야한다.

실제로 keras는 Tensorflow와 독립적으로 개발된 라이브러리 였으며, 이후 TensorFlow에 통합되어 `tf.keras.loss `처럼 `.`을 이용해 표현하게 되었다. 해당 이름을 모두 암기하기보다는 쓸 때마다 찾아서 써보기로 하자.
classification 문제가 아니라 regression 문제를 해결하려는 경우. loss를 `MeanSquaredError()`로 바꿀 수 있으며, 이 경우에 TensorFlow는 Mean squared error function을 minimize하려고 시도한다.
loss를 정했으니, 모든 m개의 training example에 loss의 평균을 취하고, 나온 cost function을 최적화하면 binary classification 문제에 neural network를 맞출 수 있다.
정의된 cost function은 아래와 같다. $J(W,B)$에 있는 대문자 bold W는 각 layer의 matrix W를 모아둔 matrix로 생각할 수 있으며, $B$ 또한 각 layer의 $\vec {b}$를 모아둔 matrix로 생각할 수 있다.
$W,B$를 기준으로 cost function을 optimize하는 경우 신경망의 모든 parameter를 기준으로 optimize한다는 뜻이며,
neural network의 출력이 모든 계층의 모든 parameter에 따라 달라진다는 점을 강조하기 위해서 아래 첨자를 붙여 $f_{W,B}(\vec{x})$로도 쓸 수 있다.

3. Gradient descent
마지막으로, Tesonflow에 cross entropy function을 최소화하도록 요청해야한다.
이를 Gradient descent를 통해 수행한다.
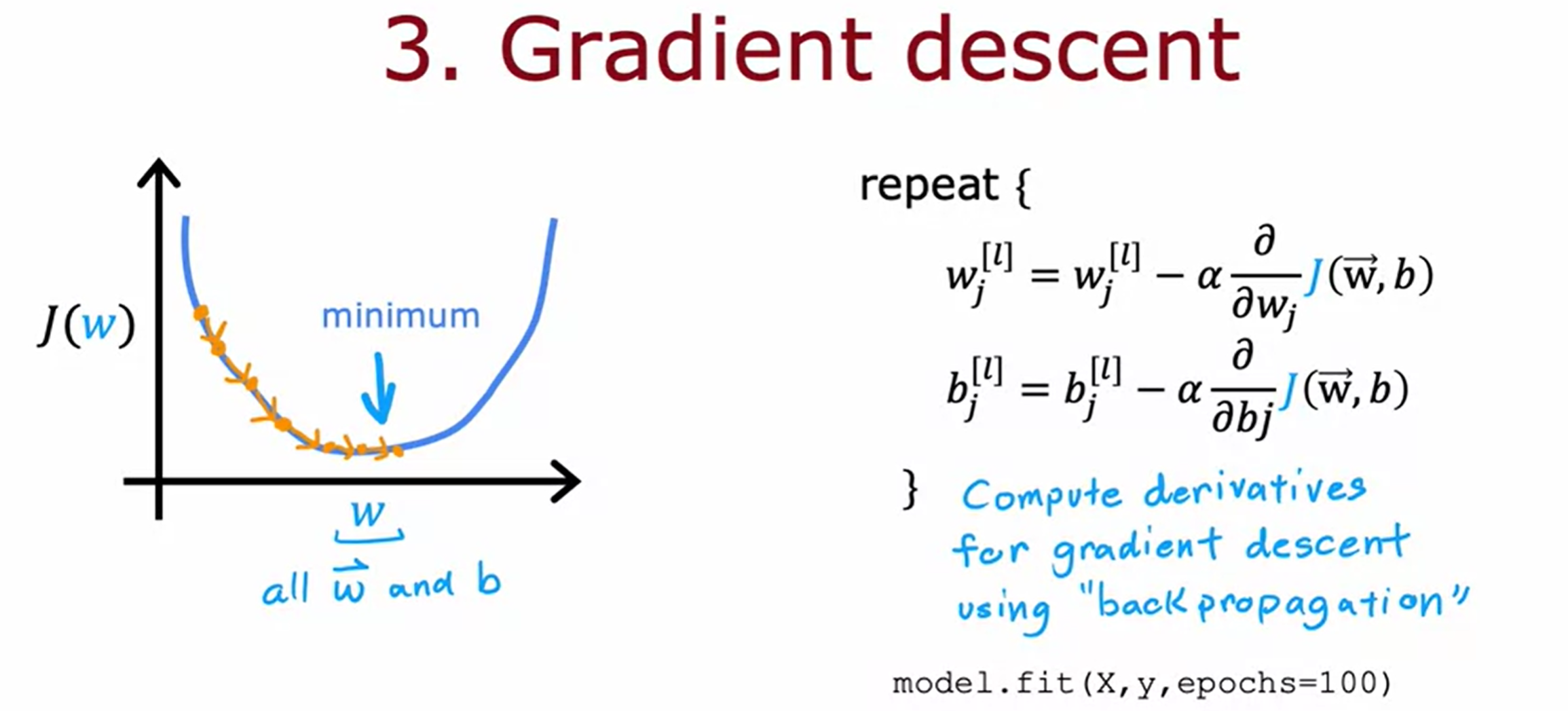
gradient descent를 수행하기 위해서는 derivative term을 계산하는 것이 중요하다. 모든 layer와 모든 unit에 대해서 parameter를 반복적으로 update해야한다.
derivative term을 계산하기 위해서 쓰이는 표준 알고리즘으로는 back propagation이라는 알고리즘을 사용하며, tensorflow는 `fit()`이라는 함수를 통해 back propagation을 모두 구현한다. training set `X`,`y`와 `epoch`을 지정하여 `fit()`함수를 수행하면 Tensorflow가 작업을 대신 수행해준다.
기술이 발전함에 따라서 라이브러리가 많이 발전하였으며, 위에서 알아봤듯이 Tensorflow는 다양한 기능을 지원해준다.
따라서 현재는 대부분의 개발자가 Tensorflow와 같은 라이브러리를 사용한다.

오늘날의 neural network 구현에서는 Tensorflow나 Pytorch같은 라이브러리를 사용한다.
그러나, 라이브러리 만을 사용하기 보다 내부 연산 과정을 이해하는 것이 model을 개선하는 데 더 좋을 것이다.
Activation Functions
Alternatives to the sigmoid activation
지금까지 모든 hidden layer와 output layer의 모든 unit에서 sigmoid activation function을 사용했다.
sigmoid뿐 아니라 다른 activation function을 사용하면 neural network를 더욱 강력하게 만들 수 있다.
Demand prediction의 예시를 떠올려 보자.

여기서 awareness(인지도)는 아예 모르는 것, 조금 아는것, 많이 아는 것과 같이 정도를 나눌수 있으며, 이는 0과 1같이 이분법적으로 판단하기에는 어려움이 있다. 따라서 0, 1과 같은 binary로 modeling하거나, 0과 1사이의 숫자로 awareness를 modeling하는 것보다는 음수가 아니고, 0에서 매우 큰 숫자까지 다양할 수 있는 새로운 activation function을 정의하는 것이 더 좋다.

다시말해, 이전에 우리는 activation function으로 sigmoid를 선택했는데, $a_2^{[1]}$가 훨씬 더 큰 양수 값을 가지게 하려면 다른 activation function으로 바꾸면 된다.

일반적으로 선택되는 것은 오른쪽과 같은 함수이며, 해당 activation function의 이름은 ReLU함수이다.
ReLU함수는 아래와 같은 식으로 표현한다.
$$g(z) = max(0,z)$$
Relu는 Rectified Linear Unit의 약어이다. 이렇게 생긴 g(z)를 지칭하기 위해 대부분 풀네임보다는 ReLU[렐루]라고 부른다.
z<0일 때는 g(z)의 값이 0이며, flat한 지점을 가진다.
z>=0일 때는 g(z) = z이며, 선형적인 지점을 가진다. ReLU 함수를 이용하면 $a_2^{[1]}$같은 activation value는 0이나 음수가 아닌 값을 가질 수 있게 된다.
이처럼 g(z)에 무엇을 사용할지는 선택할 수 있으며, sigmoid activation function외에도 다른 함수를 사용할 수 있다는 점을 파악하고 넘어가자.

ReLU 외에도 다른 activation function 또한 존재한다.
이것은 Linear activation function이며, $g(z)=z$의 값을 가진다.
즉, Linear activation function의 $g(z)$값은 $wx+b$와 같기 때문에, activation function을 사용하지 않고 있다고 말하기도 한다.
-> 이 때문에 Linear activation function은 No activation function이라고 하기도 한다.
강의에서는 linear activation function이라는 용어를 선택한다.
Choosing activation functions
위와 같은 다양한 activation function이 존재할 때, neuron에 대한 적절한 activation function은 어떻게 선택하는 것이 좋을까?
먼저, output layer의 activation function에 대해 살펴보자.
Activation function for Output layer
output layer에서는 target label y에 따라 activation function을 자연스럽게 선택할 수 있는 경우가 많다..

- binary classification -> sigmoid
- Regression 문제, y가 음수와 양수의 값을 둘 다 가지는 경우-> Linear activation function
linear activation function은 y가 양수일수도, 음수일수도 있으므로 linear activation function을 선택한다. - Regression 문제, y가 non-negative value(음수가 아닌 값)만을 가지는 경우 -> ReLU
ReLU 함수는 음수가 아닌 0이나 양수의 값만을 취하기 때문이다.
즉, 이처럼 output layer에 사용할 activation function을 선택할 떄는 일반적으로 예측하려는 label y가 무엇인지에 따라 선택한다.(Andrew Ng 교수님도 위의 지침을 자주 선택하신다고 한다.)
Activation function for hidden layer
hidden layer에서는 어떤 activation function이 사용될까?
결론적으로는, hidden layer에는 ReLU activation function을 사용하는 것이 좋다.

이전 강의에서 neural network를 구축할 때 sigmoid function을 통해 설명했지만, hidden layer에 sigmoid function은 거의 사용하지 않는다.
결국 sigmoid function은 neural network에서 거의 사용되지 않으며, 오직 Binary classification의 경우에만 output layer에서 sigmoid function이 사용된다.
그렇다면 왜 sigmoid function을 사용하지 않을까?

먼저 ReLU와 sigmoid를 비교해보면 1. ReLU는 최댓값 0,z만 계산하면 되기 때문에 sigmoid보다 계산 속도가 더 빠르다.
더 중요한 것은 2. ReLU 함수가 그래프의 한 부분에서만 평평하다는 점이다.
ReLU 함수에서는 왼쪽 부분 하나만 flat하지만, sigmoid에서는 두 지점에서 flat하다. activation function은 cost function에 들어가는 함수의 일부이기 때문에, activation에 flat한 지점이 많다면 cost function J에도 기울기가 작고 평탄한 위치가 더 많아져서 학습 속도가 느려진다. 즉, gradient descent를 이용하여 neural network를 훈련 시키는 경우, flat한 지점을 많이 가지고 있는 함수라면 gradient descent의 속도는 매우 느릴 것이다.
ReLU activation function을 사용하면 neural network를 조금 더 빠르게 학습할 수 있기 때문에 ReLU가 가장 일반적인 선태이 되었다.
다시 요약하자면, model을 구축할 때 추천하는 방법은 아래와 같다.

Output Layer의 경우
- Binary classification -> `sigmoid`
- regession, y가 negative/positive value 둘 다 가짐 -> `linear` activation function
- regression, y>=0 인 값만 가질 때 -> `relu`
hidden layer의 경우
- ReLU를 기본 activation function으로 사용하기.
즉, Binary classification의 경우를 구현하자면, 위처럼 hidden layer에는 Relu를 사용하고, Output layer의 activation만 예측하려는 y에 따라 바꿔주면 된다.
연구 문헌을 보다보면, 또다른 activation function을 사용하기도 한다,
ex. LeakyReLU, tan 등등
하지만, 대부분의 분야에서는 위와 같은 지침을 따르면 충분하다. 다른 activation function이 조금 더 잘 작동하는 경우는 몇 개 없기 때문이다.
Why do we need activation functions?
좀 더 본질적인 질문으로 돌아가보자.
그럼 neural network에 activation function은 왜 필요할까?
그리고 linear activation function만 사용하는 것은 왜 안될까?
Demand prediction의 예제를 떠올려보자.
neural network의 모든 unit에 linear activation function을 사용하면 어떻게 될까?

이 경우. 전체의 neural network는 그저 linear regression을 수행하는 것과 다를바가 없으며,
linear regression보다 복잡한 문제는 해결할 수 없게 된다.
더 간단하게 예를 들어보자.
input feature가 하나의 값만을 가지고, 각 layer의 unit도 하나씩만 존재하는 경우를 가정해보겠다.
-> input이 하나씩이니, activation또한 하나의 scalar 값만을 가진다.

모든 unit의 activation function을 liear activation으로 설정하는 경우,
각 unit의 activation value는 이전 layer의 activation을 input으로 받아 $wx+b$의 수식을 적용한 것과 같다.
$\vec{a}^{[1]}$ 를 $\vec{a}^{[2]}$ 의 input에 대입하면, $\vec{a}^{[2]}$ 는 3번째 식과 같이 나타난다.
대입 이후 나타난 weight와 bias부분을 $w,b$로 치환한다고 하면,
$\vec{a}^{[2]}$ 는 input x의 linear function일 뿐이며, 결국 neural network를 만드는 것보다, lienar regression model을 사용하는 것이 나은 상황이 발생하게 된다.
선형대수적으로, 선형함수의 선형함수는 선형함수라는 사실에서 비롯되며, 이것이 neural network에 여러 layer가 있다고 해서 linear function보다 더 복잡한 feature를 계산하거나 학습할 수 없는 이유다.
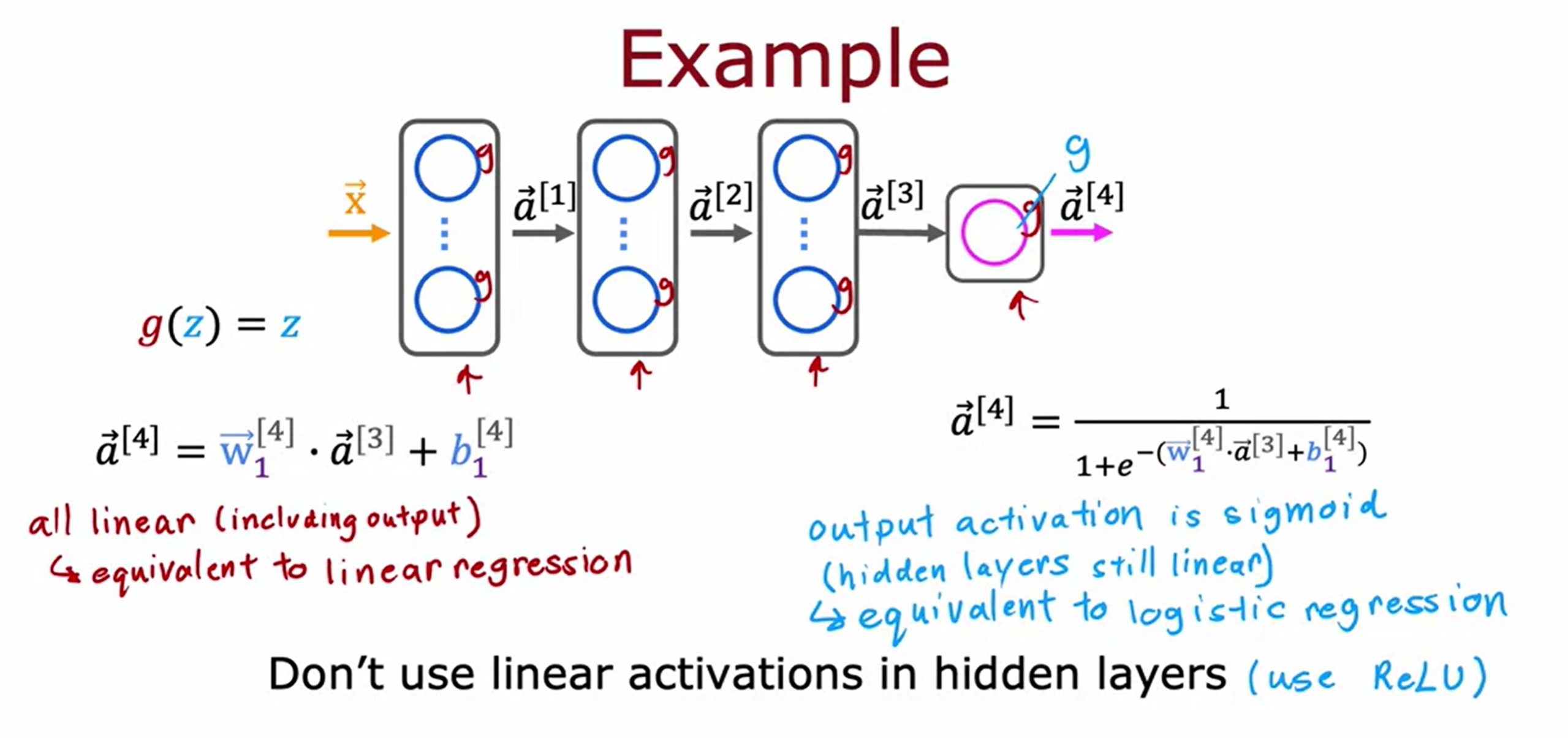
따라서 일반적인 경우에 모든 hidden layer에 linear activation function을 사용하고 output layer에 linear activation function을 사용한다고 가정하면, 이는 결국 linear regression과 동일한 출력값을 계산하게 된다.
(따라서 $\vec{a}^{[4]}$역시 input x와 b에 대한 linear function으로 표시할 수 있다.)
모든 hidden layer에 linear activation function을 사용하고 ouput layer가 sigmoid activation function을 사용하는 경우에도 이는 logistic regression의 출력과 같아지게 되며, logistic regression으로 할 수 없는 작업은 수행할 수 없게 된다.
즉, 보통 ReLU activation function을 사용하는 것이 좋다.
이것이 왜 하나의 activation function말고도 다양한 activation function이 필요한지에 대한 이유이다.
Relu의 non-linear한 부분이 필요한 이유
Relu의 왼쪽 부분은 flat한 지점이며, 이 부분으로 인해 ReLU함수는 non-linear한 function이 되게 된다.
ReLU의 non-linear한 부분은 복잡한 non-linear 함수를 이루는데 많은 영향을 미친다.
ReLU함수는 flat한 부분에서 linear한 부분으로 이어지며, 이 지점은 함수의 값이 변하는 전환점의 역할을 한다.
즉, non-linear한 부분이 존재하기 때문에 전환점을 기준으로 전환점 이전의 입력과 전환점 이후 입력을 구분할 수 있다.
이를 ReLU함수의 "off"라고도 표현하는 것 같다.
따라서 ReLU 활성화의 "끄기" 또는 비활성화 기능을 사용하면 모델이 선형 세그먼트를 함께 연결하여 복잡한 비선형 함수를 모델링할 수 있게 된다. 자세한 점은 lab 부분을 참고하도록 하자.



