Coursera의 Machine Learning Specialization강의를 정리한 내용입니다
Multiclass
Multiclass classification은 output label이 0이나 1만 가지는 것이 아니라 2개 이상의 output label을 가지는 classification 문제이다.

사진을 보면, binary classificaiton과 달리 숫자를 10개나 구분해야한다.
Multiclass classification은 여전히 y가 소수의 불연속적인 category를 가진다는 점에서 classification 문제이지만,
target y가 2개 이상의 값을 가질 수 있다는 것이 binary classification과의 차이점이다.
예시를 좀 더 살펴보자.
- example

이전에 classifcation과 관련된 문제에서는 feature x가 주어지면 y가 1이될 확률을 추정하였다.

multiclass classification 문제에서는 공간을 2개의 class로 나누것이 아니라 여러 개의 class로 나눌 수 있다.
다시 말해, y=1이 될 확률뿐 아니라, y=3이 될 확률, y=4가 될 확률과 같은 여러 개의 class를 만들 수 있다.
이런 multiclass classification문제에는 softmax regression알고리즘을 이용하여 해결할 수 있다.
Softmax
softmax regression 알고리즘은 multiclass classification을 위해 logistic regression을 generalization(일반화)한 것이다.

logistic regression은 output label로 2개의 출력값을 가질 수 있을 때 적용되었음을 배웠다.
z는 w와 x의 dot product에 b를 더한 것으로 계산된다.
또한, 우리는 logistic regression에서 도출된 $g(z)$가 $a_1$(activation)과 같음을 계산했다.
(모든 경우의 수에 대한 확률을 더하면 1이므로, $a_1$의 값이 0.71이라면, $a_2$의 값은 0.29여야한다.)
따라서, $a_2$는 $1-a_1$으로 나타낼 수 있다.
이제 이것을 softmax regression으로 generalization해보자.
y가 4개의 output을 받아 1,2,3,4중 하나를 가질수 있는 경우를 예를 들어보겠다.

softmax regression은 위와 같이나타난다.
각 class별로 파라미터와 z가 존재하며 계산되는 a는 y가 해당 class일 때 $e^{z_j}$의 값을 모든 class의 $e^{z_j}$를 합친 값으로 나눈 값을 가진다. 또한, 여기에서도 모든 경우의 output을 합산하면 1이 되어야한다.

즉, 위와 같은 공식으로 계산할 수 있다.
output이 n개의 가능한 label을 가질 때, softmax regression에서
- $z = \vec{w_j} \cdot \vec{x_j} + b$
- 각각의 output(activation은 output을 나타냈었다)은 위와 같은 공식으로 계산
- n개의 경우의 output을 모두 합산하면 1이다.
만약 output label이 2개뿐이라면, softmax는 기본적으로 logistic regression과 같은 결과를 계산하게 된다.
-> 이때문에 softmax regression이 logistic regression의 generalization이라고 한다.
Cost

기존의 logistic regression의 loss와 cost는 왼쪽과 같았다.
(cost는 loss의 전체 평균이었다.)
softmax regressino에서 사용하는 방정식은 오른쪽과 같다.
a에 대한 식은 위에서 알아보았던 것과 같으며, n개의 class를 가진다고 가정했을 때 위와 같이 나타난다.
또한, soft max regression에서는 아래와 같은 loss를 사용한다.
$y=1$이라면 loss는 $-log\,{a_1}$로 나타나며, $y=2$라면 loss는 $-log\,{a_2}$로 나타난다.

즉, $y=j$라면 loss는 $-log\,{a_j}$로 나타날 것이다.
$a_j$(x값)가 1에 매우 가까우면 loss는 매우 작아질 것이고, $a_j$가 작아질 수록 loss는 커진다.
이를 통해 알고리즘은 $a_j$를 최대한 1에 가깝게 만들려고 할 것이다.
-> 이는 y가 해당 값일 확률이 높다는 것을 말한다.(ex. $a_2$가 높은 것은 y=2일 확률이 높다는 것을 말한다.)
유의할 점은 각 training example의 y는 하나의 값만 가질 수 있다는 것이다.
즉, 특정 training example에서 $y=2$라면 $j=2$ 인 경우인 $-log\,{a_2}$만 계산하며, $-log\,{a_1}$과 같은 다른 항은 계산되지 않는다.
Neural Network with Softmax output
multiclass classification을 수행할 수 있는 neural network를 구축하기 위해 Softmax regression model을 가져와서
Output Layer에 넣을 것이다. <- hidden layer에는 ReLU를 넣는 것을 지난 시간에 학습했다.

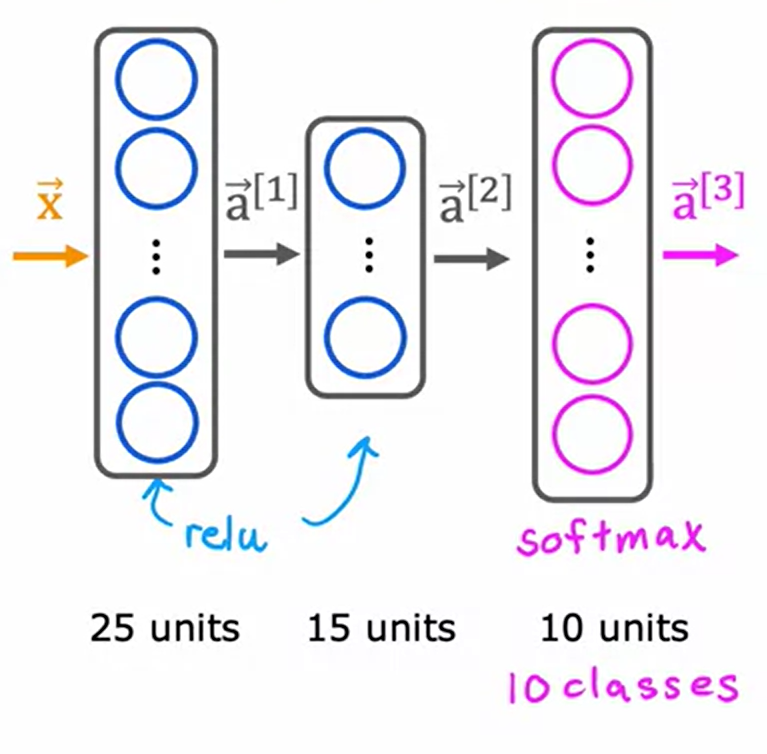
이전에 2개의 class를 분류하던 손글씨 인식문제와는 다르게, 0~9까지의 10개의 class로 늘어났으며, 10개의 class를 분류해내기 위해 오른쪽과 같이 10개의 output unit을 갖도록 output layer가 변경된다.
이 새로운 output layer는 softmax의 output layer가 되며, neural network에서 softmax output이 존재하는 layer를 softmax layer라는 용어로 말하기도 한다.
softmax layer전까지의 계산과정은 이전과 동일하게 진행된다.

출력 class가 10개인 경우 위와 같이 계산이 진행된다.
각 unit 별로 softmax regression을 진행한 값을 activation value로 가지며, 아래 첨자를 통해 $z_1,z_2...z_{10}$과 $a_1,a_2...a_{10}$으로 나타낼 수 있다.
이렇게 하면 y의 10번째 label까지 $y=1, y=2..$일 확률을 추정할 수 있다.
(위 첨자를 통해 layer3과 관련된 quantity임을 나타낸다.)
softmax layer는 softmax activation function이라고도 불린다.
기존의 linear, logistic과 같은 activation function은 $a_1=g(z_1)$, $a_2=g(z_2)$처럼 하나의 z에만 영향을 받았었다.

그런데, softmax activation function은 $z_1$~$z_{10}$처럼 모든 label의 z값을 사용하며, 각 activation 값은 z의 모든 값에 따라 달라진다.
마지막으로 Tensorflow에서 이를 구현하는 방법을 살펴보겠다.

1. 모델 정의, 2. loss와 cost 구체화, 3. cost J를 최소화
위와 같은 과정을 수행하는 것은 동일하다.
단, loss에서는 `SparseCategoricalCrossentropy`함수를 호출한다.
(sparse(희소)는 y가 10개의 값중 하나만 가질 수 있다는 것을 의미한다. ex. 숫자 2와 7이 동시에 있는 사진은 볼 수 없다.)
- 주의!!! 위의 코드는 사용하지 말자
Tensorflow에서는 더 잘 작동하는 버전이 있기 때문에 위의 코드는 사용하지 말자. 그냥 어떻게 진행되는지 로직만 파악하자.
Improved implementation of softmax
위와 같은 구현에서 어떤 문제가 발생할 수 있는지, 그리고 이를 개선할 수 있는 방법을 살펴보도록 하자.

컴퓨터에서는 숫자를 계산하는 2가지 방법이 있다.
첫번째처럼 값을 단순히 설정하는 것과, 두번째처럼 계산한 식들끼리 빼는 것이다.

컴퓨터에는 각 숫자를 저장할 수 있는 메모리가 한정되어 있기 때문에, round-off error(반올림 오차)는 두번째와 같이 계산한 식들끼리 빼는 과정에서 발생할 수 있다.
이를 위해, Tensorflow 내에서 더 정확한 계산을 할 수 있도록 공식화된 방법이 있다.

logistic regression를 계산할 경우, 위와 같은 기본적인 코드를 가졌었다. (원래의 과정은 식끼리 빼는 계산을 수행하는 것과 같다)
하지만, Tensorflow를 사용하면 a를 중간항으로 계산할 필요가 없다.

위의 사진은 a를 가져다가 원래의 식으로 확장한 것 뿐이다. 이 방법으로 Tensorflow는 loss를 수치적으로 더 정확하게 계산할 수 있다.
이러한 작업을 수행하는 코드는 아래와 같다.

1. output layer의 activation function을 `linear`로 변경 후
2. `model.complie`의 과정에서 `BinaryCrossEntropy`의 인자로 `from_logits=True`를 주는 것이다.
`logit`은 $z$를 뜻한다. Tensorflow는 $z$를 중간항으로 계산하지만,위의 방식으로 더 정확하게 계산하도록 항을 재배열 할 수 있다.
마찬가지로 softmax에서도 round-off error가 발생할 수 있으며,
rearrange term을 사용함으로써 에러가 매우 커지거나 작아지는 것을 막는다.

위와 같이 나타낼 수 있다.(logistic의 수치 정확도 높이는 방법과 같다.)
수치적으로 조금 더 정확하다는 것을 빼면, 처음에 보았던 기존 코드와 동일한 기능을 한다.

output layer의 softmax activation을 `linear`로 변경했기 때문에, 신경망의 output layer는 더이상 $a_1$~$a_10$의 확률을 출력하지 않고 $z_1$~$z_10$을 출력한다. 따라서, 실제 확률을 구하기 위해서는 마지막에 softmax함수를 호출하여 output을 출력해주는 과정이 필요하다.

logistic regression의 경우에도, 마지막에 sigmoid 함수를 호출해서 해당 함수를 통해 출력하도록 코드를 변경해주어야한다.
Classification with multiple outputs(Multi label classification)
Multiclass Classification과 쉽게 혼동할 수 있는 것은 Multi label classification이라고 불리는 Classification 문제이다.

단일 입력과 관련된 image x는 이미지에 자동차, 버스, 또는 보행자가 있는지 여부에 해당하는 3개의 서로 다른 레이블을 가질 수 있다.
이 경우에 target y는 실제로 3개의 값으로 구성된 vector이다. multiclass classification에서의 target y는 하나의 single value를 가졌던 것과는 차이가 있다.
multi-label classification 문제를 해결하려면 어떻게 해야할까?
- 완전히 분리된 3개의 problem으로 처리한다.(처음엔 자동차를 탐지, 두번째엔 버스를 탐지, 세 번째엔 보행자를 탐지)

- 자동차, 버스, 보행자 세 개를 동시에 감지하도록 neural network를 훈련 시키는 것(즉, 3개의 Output을 가짐)

우리는 2번 방법을 선택할 것이다.
output layer의 3개의 노드 각각에 sigmoid activation function을 사용할 수 있으며, 이 경우에 $\vec a^{[1]}$는 3개의 output을 가진 vector가 된다.
Multiclass classification과 multi-label classification을 혼동하면 안된다!
다시 한번 정리하고 넘어가자.
multi class
- 마지막 output이 1개이다.
- multi-class를 분류하기 위해 output layer에 neuron이 여러개 존재하지만, 발생한 여러개의 output중에서 해당하는 하나의 class의 output 말고 나머지는 모두 무시됨.
-> 즉, 마지막 class 하나만 output으로 가짐
multi label
- 마지막 output이 여러개가 나올 수 있으며 각각의 output마다 sigmoid 계산한다.
->즉, 여러 개의 label을 output으로 가질 수 있음



