Coursera의 Machine Learning Specialization강의를 정리한 내용입니다
Is there a path to AGI?
AI는 매우 다른 2가지의 ai를 포함한다.
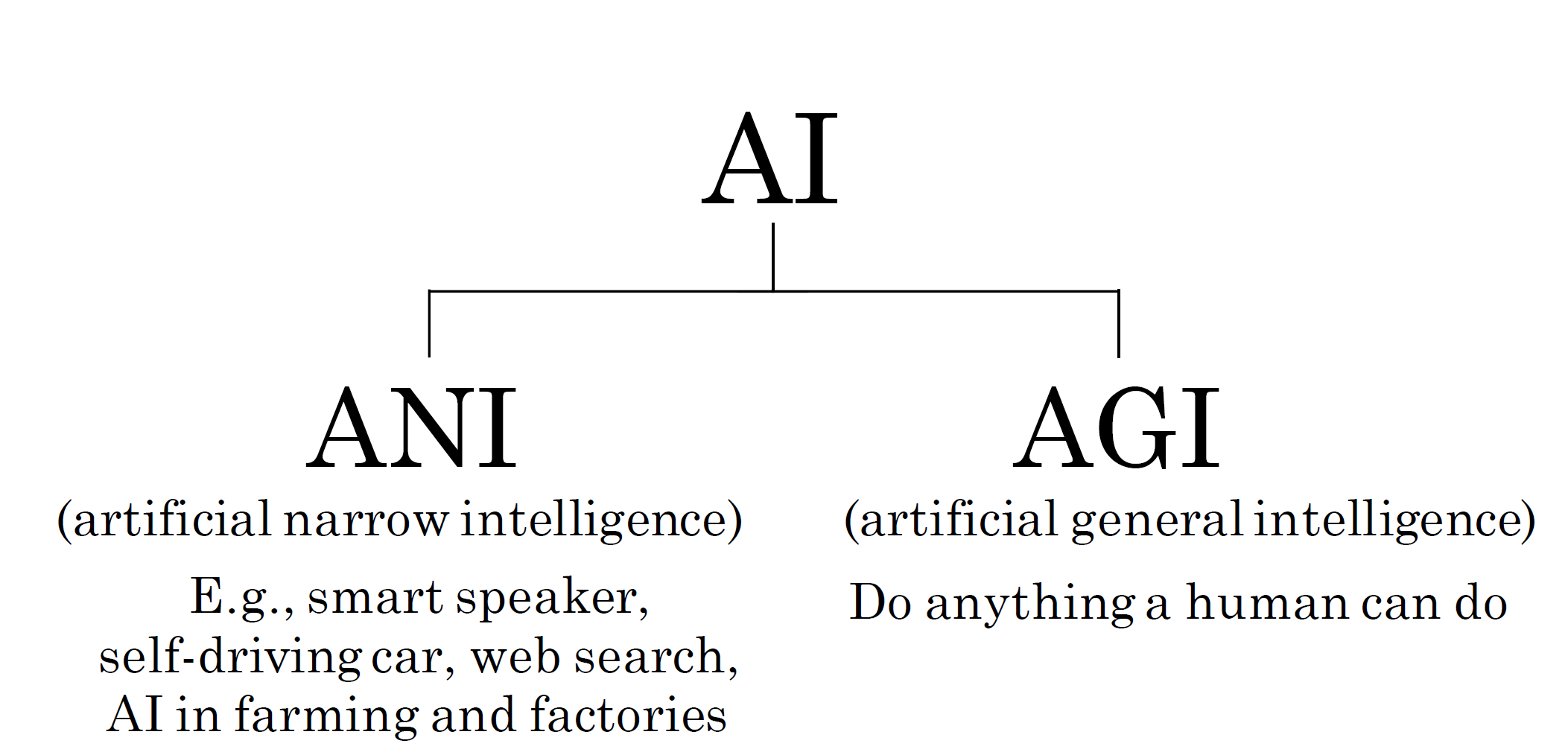
ANI는 artificial narrow intelligence의 약자로, 특정 응용 분야, 즉, 좁은 작업에 적용되는 AI system이다.
AGI는 artificial general intellignece의 약자로 사람이 할 수 있는 모든 일을 할 수 있는 AI system이다.
지난 몇년동안 ANI는 엄청난 발전을 이루었다. 따라서 ANI의 진전으로 현재 AI가 많은 발전을 이루었다는 것은 과언이 아니다.
그러나, AI에 큰 발전이 있었다는게 꼭 AGI에 대한 발전이 있었다는 걸 뜻하진 않는다.
수년전부터, neuron을 시뮬레이션할 수 있었고, 지능적인 시스템을 만들 수 있는 희망이 있다고 생각했지만, 그렇게 간단하지 않은 작업임이 드러나게 되었다.
그 이유는 2가지 정도로 생각할 수 있다.
1. artificial neural network는 매우 단순화된 버전이라 실제 생물학적 neuron이 하는 것과는 전혀 다르다.
2. 우리는 뇌가 어떻게 작동하는지 거의 모른다.
따라서 AGI로 가는 길은 매우 어려운 일이다.


그렇다면 AGI는 불가능한 일일까?
이에 대해 Andrew Ng 교수님은 AGI의 희망이 있다는 다양한 증거를 보여주신다.


먼저, 첫번째 사진을 살펴보자
해당 실험에서는 뇌의 한부분인 청각 피질(Auditory cortex)에 대한 연구가 있었다.
귀에서 어떤 소리를 감지하느냐에 따라 전기자극의 형태로 귀에서 오는 신호를 전달받는 청각피질과 귀의 연결을 끊고, 청각피질에 시각적 정보를 입력하면 청각피질이 보는 법을 배우게 된다는 것이 밝혀졌다.
또한, 체성 감각 피질(촉각처리를 진행)과 촉각에 대한 연결을 끊고 대신 시각적 정보를 입력하도록 구성하면 이번엔 체성감각 피질이 보는 법을 배우게 된다.
즉, 뇌의 다양한 부분이 data에 따라 보고나 느끼는 법을 배운다는 사실을 알 수 있다. 이는, 주어진 데이터에 따라 유동적으로 입력값을 처리할 수 있다는 것이다.

또한, 카메라를 혀에서 느껴지는 전압 패턴에 매핑하면 눈이 먼 사람도 혀로 보는 법을 배울 수 있고,
이뿐 아니라 수중 음파 탐지기를 통해 보는 법, 방향감각을 얻게 되는 Haptic belt, 개구리에게 3번째 눈을 이식하여 학습하는 실험들이 있었다. 즉, 이는 뇌가 입력되는 감각의 다양성에 적응할수 있다는 것이다.
AGI에 대한 연구는 아직도 진행중이며, AGI를 추구하지 않더라도 neural network는 애플리케이션을 구축할 수 있는 매우 강력한 도구라고 할 수 있다.
How neural networks are implemented efficiently
neural network는 vectorization이 가능하기 때문에 matrix multiplecation(행렬곱셈)을 이용하면 매우 효율적으로 구현할 수 있다.

왼쪽은 이전에 살펴본 forward propgation을 구현하는 코드이다.
`W`에서 각 column별로 $w_j$파라미터를 가졌었다.
위와 같은 코드를 vectorized하여 구현할 수 있다.
1-D array였던 것들은 2중 대괄호를 사용하여 모두 2-D array(matrix)로 변환해준다.
이후, dense 입력으로 들어가는 것들은 모두 matrix라는 것에 유의하자.
matrix multiplication같은 경우는 `np.matmul`을 이용하여 수행한다.
for 문을 통해 길게 반복하던 부분을 vectorization을 통해 간략하게 나타낼 수 있다.
Matrix multiplication

matrix는 숫자로 구성된 2-D array였다.
두 matrix를 곱한다는 것은 무엇을 의미할까?
우선 dot product(내적)를 계산하는 방법을 살펴보면, index가 같은 element끼리 곱한 후 합산한다.
이를 일반적으로 column vector끼리의 dot product로 작성할 수 있다.
또한, transpose를사용하여 column vector를 row vector로 바꿀 수 있다.
transpose란 column vector를 가져와서 옆으로 배치하는 것을 의미한다. (위첨자에 대문자 T를 통해 나타낸다)
z는 a의 transpose에 w를 곱하는 것(행렬의 곱)으로 생각할 수 있으며, 이는 기존 vector a와 w의 dot product(내적)와 동일하다.
transpose를 사용한 식으로 나타내면 아래와 같다.
이제 vector에 transpose를 취해 matrix를 곱하는 vector matrix multiplication(vector*matrix)에 대해 자세하게 살펴보자


마찬가지로 vector a를 transpose 시킨 후, matrix W와의 곱을 구한다.
matrix W의 각 column은 $w_1,w_2...w_n$에 해당하므로
transpose값과 각 column vector를 곱한 후 합산하면 Z를 구할수 있다.
비슷한 방식이지만, 이번엔 matrix matrix multiplication에 대해 알아보자(행렬간 곱셈)


먼저, 동일하게 matrix A를 transpose 시킨다.
이후 transpose A의 row별로 W의 column과의 곱셈을 진행하면 된다.
Matrix multiplication rules
이제 두 matrix를 곱하는 일반적인 형식을 살펴보자.

앞서 말했듯, matrix의 각 column을 vector로 생각해보자.
즉 3개의 vector가 만들어지며, 이를 transpose 시키면 위와 같이 나타낸다.
(각 column을 가져와서 옆으로 나열하면 된다.)
A와 W의 matrix 모두에 약간의 음영을 주었는데, 동일한 음영은 같은 vector로 그룹화된 숫자들을 뜻한다.
맨 오른쪽의 선은, Z의 element가 어떤 행과 열에 영향을 받는지를 나타낸 것이다.

예를 들어 동그라미 친 부분을 계산한다고 해보면 위와 같은 계산과정이 진행됨을 파악할 수 있다.

matrix multiplication에서 중요한 규칙과 특징은 아래와 같다.(아래 사진에서도 확인할 수 있다)
- matrix $A$와 matrix $B$를 곱한다고 가정할 때,
$A$의 column과 $B$의 row의 크기는 일치해야한다. - 곱을 통해 만들어진 matrix의 크기는 transpose A의 row by W의 column으로 나타난다.


Matrix multiplication code
matrix multiplication을 code로는 어떻게 구현할 수 있을까?
matrix끼리의 곱셈이니 이중 대괄호를 사용하여 구성한다.
transpose는 numpy의 `.T` 함수를 통해 수행할 수 있다. matrix의 column을 가져와서 옆으로 배치하는 transpose함수이다.
이후 `np.matmul`함수를 사용하면 행렬의 곱셈을 수행해준다.
`@`[앳]은 `matmul`함수를 호출하는 또다른 방법이다. 그러나, 가독성을 위해 `np.matmul`을 사용하는 것이 더 낫다.

forward prop의 벡터화된 구현이 어떤 모습인지 살펴보자.
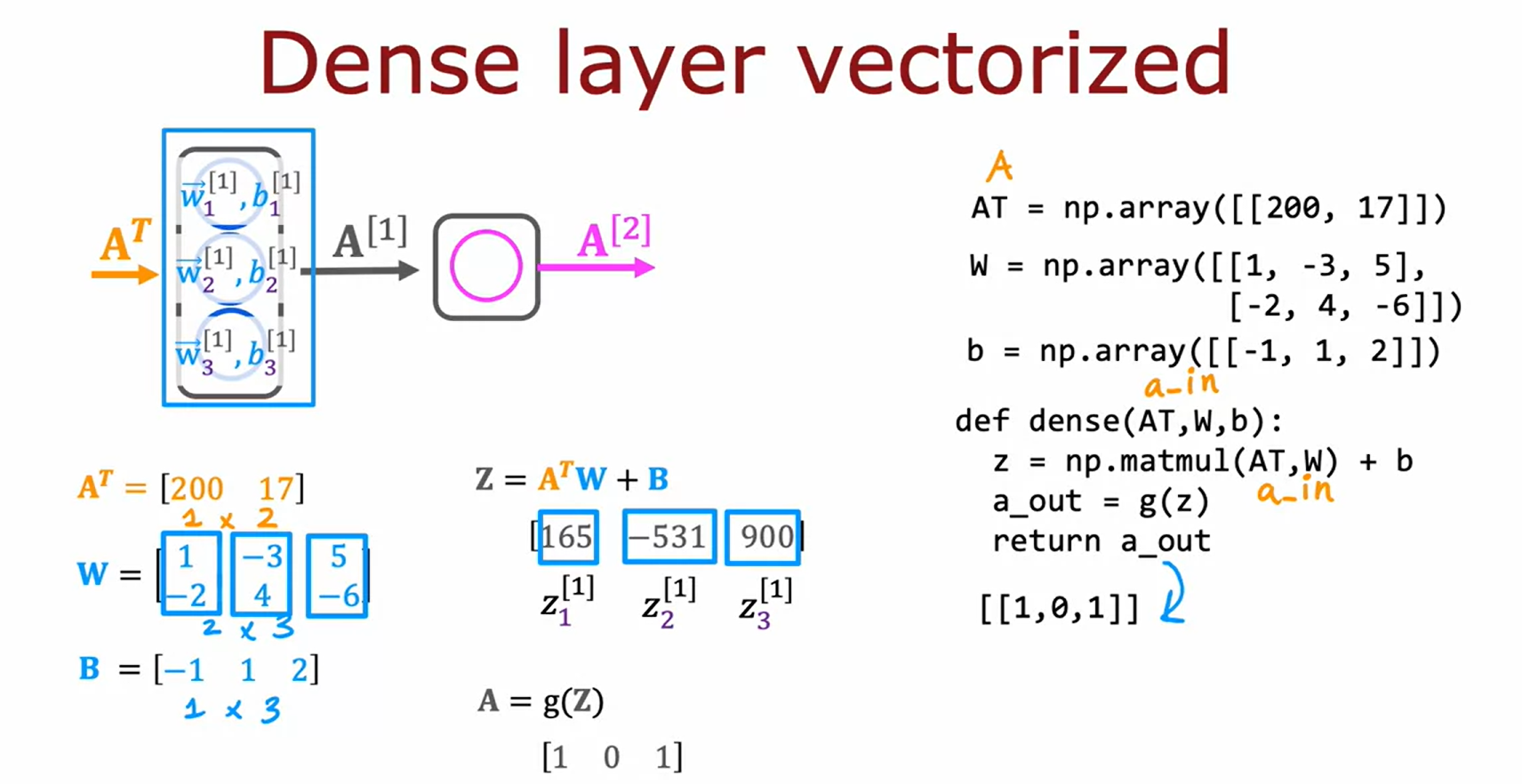
코드상에서 마찬가지로 $A^T$의 column과 $W$의 row의 size를 맞춰주어야한다.
Vectoriziation 강의 이전에 알아본 코드와 다른 점은 `a`와 `a_in`을 `AT`로 대체했다는 것뿐이다.
Numpy broadcasting
https://numpy.org/doc/stable/user/basics.broadcasting.html
Broadcasting — NumPy v2.1 Manual
Broadcasting The term broadcasting describes how NumPy treats arrays with different shapes during arithmetic operations. Subject to certain constraints, the smaller array is “broadcast” across the larger array so that they have compatible shapes. Broad
numpy.org
matrix의 곱셈이 아닌,덧셈과 관련해서는 어떻게 진행이 될까?
이를 위해서는 broadcasting을 이해해야한다.
broadcasting은 1-d array인 행렬의 dimension을 확장하는 것(row가 1이라면 column을 확장, column이 1이라면 row 확장)이다.
2개의 matrix는 아래의 경우에 비교&연산이 가능하다.
- 두 행렬이 같을 때
- 둘 중 하나가 1-d array
- matrix+scalar
예를들어, a가 (1,3) matrix이고, b가 scalar라고 하면, 아래와 같이 덧셈을 수행한다.

a = 3 x 1
b = 1
------------
r = 3 x 1
모든 element에 b의 덧셈을 구현하기 위해서, b의 개수를 a의 element만큼 늘려서(broadcasting시 element의 값은 변하지 않는다.), 모든 element에 b를 더하며 덧셈을 수행한다.
물론, 아래와 같이 a는 row에 대해, b는 column에 대해 broadcasting하여 계산할 수도 있다.

-matrix + matrix
그렇다면, dimension이 다른 matrix+matrix의 경우라면 어떻게 될까?
이 경우에도, broadcasting을 이용해야한다.
b의 row가 1이므로, a에 맞춰서 broadcasting해준다.

즉, 계산의 결과는 아래와 같이 진행된다.
- Calculating Broadcast Result shape

중요한 점은, 1-d array가 존재할 때는 해당 vector를 확장하는 것이고,
두 matrix의 size가 다를 때는 더 큰 size의 column과 row에 맞춰서 broadcasting해주어야한다.
(broadcasting은 '덧셈'과정에 사용된다. 맨 오른쪽 예를 행렬 곱으로 인한 결과로 생각하면 안된다.)



