Coursera의 Machine Learning Specialization강의를 정리한 내용입니다

Course 2에서 알아볼 내용은 아래와 같다.
- Neural networks(신경망)에 대해 알아보고 inference(추론) 또는 prediction(예측)을 수행하는 방법에 대해 살펴본다.
- neural networks을 훈련하는 방법에 대해 알아볼 것이다.
- Machine learning 시스템 구축을 위한 실용적인 조언
- Decision Trees(의사 결정 트리)
Neural networks intuition
뇌가 어떻게 작동하고 그것이 neural network와 어떤 관련이 있는지 살펴보자

Neural networks가 처음 발명되었을 때 원래의 동기는 생물학적 뇌가 학습하고 생각하는 방식을 모방할 수 있는 소프트웨어를 개발하는 것이었다. (오늘날의 신경망은 artificial neural network(인공신경망)이라고도 하며, 뇌의 학습방식과 거의 관련이 없다)
1980년대와 1990년대 초반에 인기를 얻어 손으로 쓴 숫자 인식과 같은 일부 응용 분야에서 인기를 끌었다고 한다.
2005년경부터 다시 resurgence(부활)하였으며, deep learning이라는 주제 안에 포함되어 speech(음성인식) -> images(컴퓨터 비전) -> text(nlp)로 크게 발전해왔다.
그렇다면 neural network의 모티브가 된 뇌는 어떻게 작동할까?

위의 사진은 뇌에 존재하는 Neuron(뉴런)에 대한 사진이다.
인간의 모든 생각은 뇌와 뇌에 있는 뉴런에서 비롯된다.
뉴런은 전기자극을 보내고 때로는 다른 뉴런과 새로운 연결을 형성한다.
뉴런들은 여러 전기자극을 input으로 받아 계산을 수행한 다음, 도출된 output을 다른 뉴런에 보내며, 해당 output은 다른 뉴런의 input이 될 수 있다.
즉, 여러가지 다른 상위 뉴런의 input을 받아 계산한 output을 다른 하위 뉴런의 input으로 보낼 수 있는 것이다.

위의 사진은 생물학적 neuron의 간단한 그림이다.
neuron은 왼쪽그림과 같이 cell body(세포체)로 구성되어 있으며, 중간에 nucleus(핵)을 가지고 있다.
생물학적 neuron에서는 입력 와이어를 dendrites(수상돌기)라고 하며, axon(축삭)이라고 하는 출력 와이어를 통해서 다른 뉴런에 전기자극을 보낸다.
중요한 점은 전기자극을 보내서 다른 뉴런에게 input을 줄 수 있다는 점이다.
인공신경망(artificial neural network)을 구축하기 위해 이러한 용어를 외울 필요는 없다.

artificial neural network 는 생물학적 뉴런이 하는 일에 비해 매우 단순화된 수학적 모델을 사용한다.
single(단일) neuron을 나타내는 작은 원( O )을 표시해보자.
neuron이 하는 일은 몇가지 입력을 받는 것이다.
1개 또는 더 많은 입력(숫자)을 받으며 계산 이후 또 다른 숫자를 출력하는데, 2번째 neuron의 input이 될 수 있다.
artificial neural network나 deep learning algorithm을 만들 때는 한번에 하나의 neuron을 만드는 대신
아래와 같이 여러개의 neuron을 동시에 시뮬레이션 하는 경우가 많다.

해당 neuron들이 총체적으로 하는 일은 몇개의 숫자를 입력하고, 계산을 수행하고, 다른 숫자를 출력하는 것이다.
현재 신경과학에 대한 수준으로는 뇌가 실제로 어떻게 작동하는지에 대해 아직 발견되지 않은 것들이 많으며, 이 때문에 극도로 단순화된 neuron model을 사용한다. 하지만 단순화된 neuron model을 사용하더라도 powerful한 deep learning algorithm을 만들 수 있다.
neural network에 대한 아이디어는 수십년 전부터 존재해왔는데, neural network가 발전한 것은 왜 지난 몇년 동안뿐(2005년부터 시작됐으므로)인걸까? 아래 사진은 이를 설명해주는 사진이다.

가로축은 problem에 대해 가지고 있는 data의 양을, 세로축에는 해당 문제에 적용된 learning algorithm의 성능 또는 정확도를 나타냈다.
지난 몇 십년동안 디지털화의 발전으로 우리가 사용하는 data의 양은 막대하게 커졌다.(Big data라는 용어로 표현한다)
따라서 종이에 기록하지 않고 디지털 기록을 사용하는 경우가 훨씬 많아졌으며, 많은 분야에서 digital data의 양이 폭발적으로 증가했다.
그로 인해 logistic regression이나 linear regression과 같은 traditional한 ML algorithm에서는 현재 제공할 수 있는 data의 양만큼 확장될 수 없었고, 성능을 높이기가 매우 어려웠다.
이후, 주어진 dataset으로 많은 neural network를 훈련시키면 성능이 점차 올라간다는 것이 증명되었고, 엄청난 양의 data를 활용하도록 neural network를 훈련 시키면 모든 분야에서 성능을 높일 수 있게 되었다.
deep learning에 강력한 성능을 보여주는 GPU의 발전도 deep learning algorithm이 자리 잡을 수 있게된 주요한 원동력이 되었다.
Demand Prediction (수요예측)
Demand Prediction(수요예측)의 예를 들어 neural network의 작동방식에 대해서 알아보겟다.
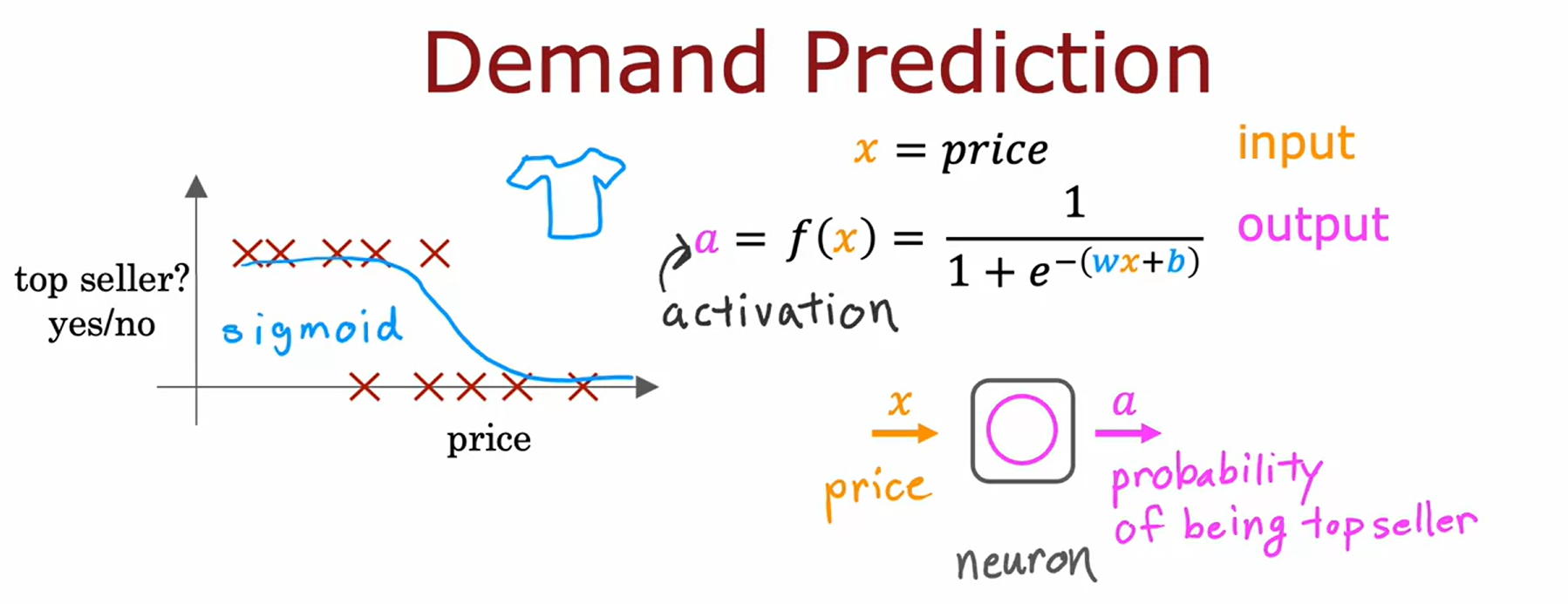
해당 예시에서는 티셔츠를 판매하고 있는데, 특정한 티셔츠가 베스트셀러가 될지 아닌지를 알고 싶다고 가정한다.
많이 팔릴 수 있는 가능성이 있는 제품을 알고 있다면, 해당 재고를 미리 구매하려는 계획을 세울 수 있기 때문이다.
input feature x는 티셔츠의 price이고, sigmoid function을 fitting하면 위와 같이 표현된다. 이전에는 이것을 learning algorithm의 output으로 $f(x)$로 작성했지만, neural network의 구축에서는 용어를 조금 바꿔 알파벳 $a$로 표현할 것이다.
a는 activation(활성화)의 약어이며, neuron이 하위의 다른 neuron에게 output을 보내는 정도를 말한다.
아래와 같이 하나의 logistic regression unit은 하나의(single) neuron의 매우 단순화된 model로 대응된다. (생물학적 neuron보다 매우 단순한 형태이기 때문에)
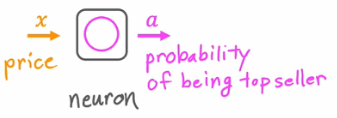
neuron이 하는 일은 price를 input으로 받아 위의 공식을 계산해서 activation을 출력하는 것이다.
즉, a는 해당 티셔츠가 베스트셀러가 될 확률이.
neural network를 구축하기 위해서는 이러한 neuron을 여러개 가져와서 연결하거나 조합하기만 하면 된다.
이제 demand prediction의 좀 더 복잡한 예를 살펴보자.

해당 예제에서는 4개의 feature를 input으로 가진다.
티셔츠가 베스트셀러가 될 지에 대한 여부는 아래와 같은 몇가지 요인에 따라 달라질 수 있다.
- affordability(경제성)
- awareness(잠재 구매자들이 이 티셔츠에 대해 어느정도 인지하고 있는지)
- perceived quality(사람들이 인식하는 옷의 품질)
총 지불 금액은 price(가격)과 shipping cost(배송비)를 더한 금액이기에 경제성은 두가지 feature와 관련있고,
awareness는 marketing과, perceived quality는 material, price(가격이 높으면 고품질로 인식하는 경우가 있다)와 관련있다.
해당 요인들과 관련된 각각의 인공 neuron을 만들어 추정해보겠다.
affordability, awareness, perceived quality에 대한 추정치를 바탕으로 세 뉴런의 output을 오른쪽에 있는 다른 neuron에 연결하면 또다른 logistic regression unit이 생기게 되는 것과 같으며, 최종적인 output을 출력해낼 수 있게 된다.(티셔츠가 베스트셀러가 될 확률)
neural network적 용어로 말하자면, 우리는 각 뉴런들을 layer라는 단위로 그룹화할 것이다.
layer란 동일하거나 유사한 feature를 입력받아 숫자 몇개를 함께 출력해주는 neuron의 group을 말한다.

중간의 layer처럼 한 layer에 여러개의 neuron이 있을 수도 있고, 오른쪽의 layer처럼 1개의 neuron만을 포함할 수도 있다.
(하나의 neuron만 가지고 있어도 layer가 될 수 있다)
최종 neuron의 output이 neural network에서 예측한 출력 확률이기에 오른쪽에 있는 layer(최종 layer)는 output layer라고도 부른다.
반대로, feature들로 구성된 목록을 input layer라고 부른다.
또한, neural network적 용어로 affordability, awareness, perceived quality를 activation이라고 부른다.
또한, 마지막의 출력 확률 또한 최종 neuron의 activation이다.
하나의 neuron이 하나의 activation을 출력하므로 activation의 개수는 neuron의 개수와 같다.
(기존의 output을 activation이라고 표현한다고 이해하자)
즉, 4개의 feature를 사용해서 activation value라고도 하는 새로운 3개의 숫자를 계산하고,
이후 output layer에서 도출된 activation value를 이용하여 하나의 숫자를 계산한다.
우리는 한번에 하나씩 뉴런을 살펴보면서 이전 계층에서 어떤 input을 받을지 결정해야했다. (affordability는 price와 shipping cost와 관련있고..등등) 그러나 어떤 뉴런이 어떤 feature를 input으로 받을지 결정하려면 너무 많은 작업이 필요하기에, 실제로 신경망은 이전 layer의 모든 feature에 접근할 수 있게 구현된다.
예를 들어, 아래와 같이 중간에 있는 layer의 각 neuron은 이전 계층인 input layer의 모든 feature에 접근할 수 있게 되며, 이후 파라미터를 적절하게 설정하여 원하는 activation과 관련이 있는 일부 기능에만 집중하는 방법을 사용한다.

neural network의 표기법과 설명을 더욱 단순화 하기 위해 위의 입력 feature 4개를 $\vec{x}$로 표현할 것이고,
3개의 activation value 또한 최종 output layer에 공급되는 또다른 vector($\vec{a}$)로 표현할 수 있다.

또한, 중간에 존재하는 layer를 "hidden layer"라고 부른다.
이 이름은 training set을 만들 때 따온 것이다,
training set은 (x,y)처럼 올바른 x에 따른 올바른 output값을 알려주지만 neuron을 몇 차례 통과한 data set은 올바른 값이 무엇인지 알려주지 않는다.
이를 올바른 값이 "숨겨져있다(hidden)"라고 표현한다.
따라서 중간에서 training되는 data set에는 올바른 값이 표시 되지 않기에 중간에 있는 layer들을 hidden layer라고 표시한다.
neural network의 직관에 도움을 주는 또다른 것은
activation을 input으로 받아들이는 logistic regression unit이 존재한다는 점이다.
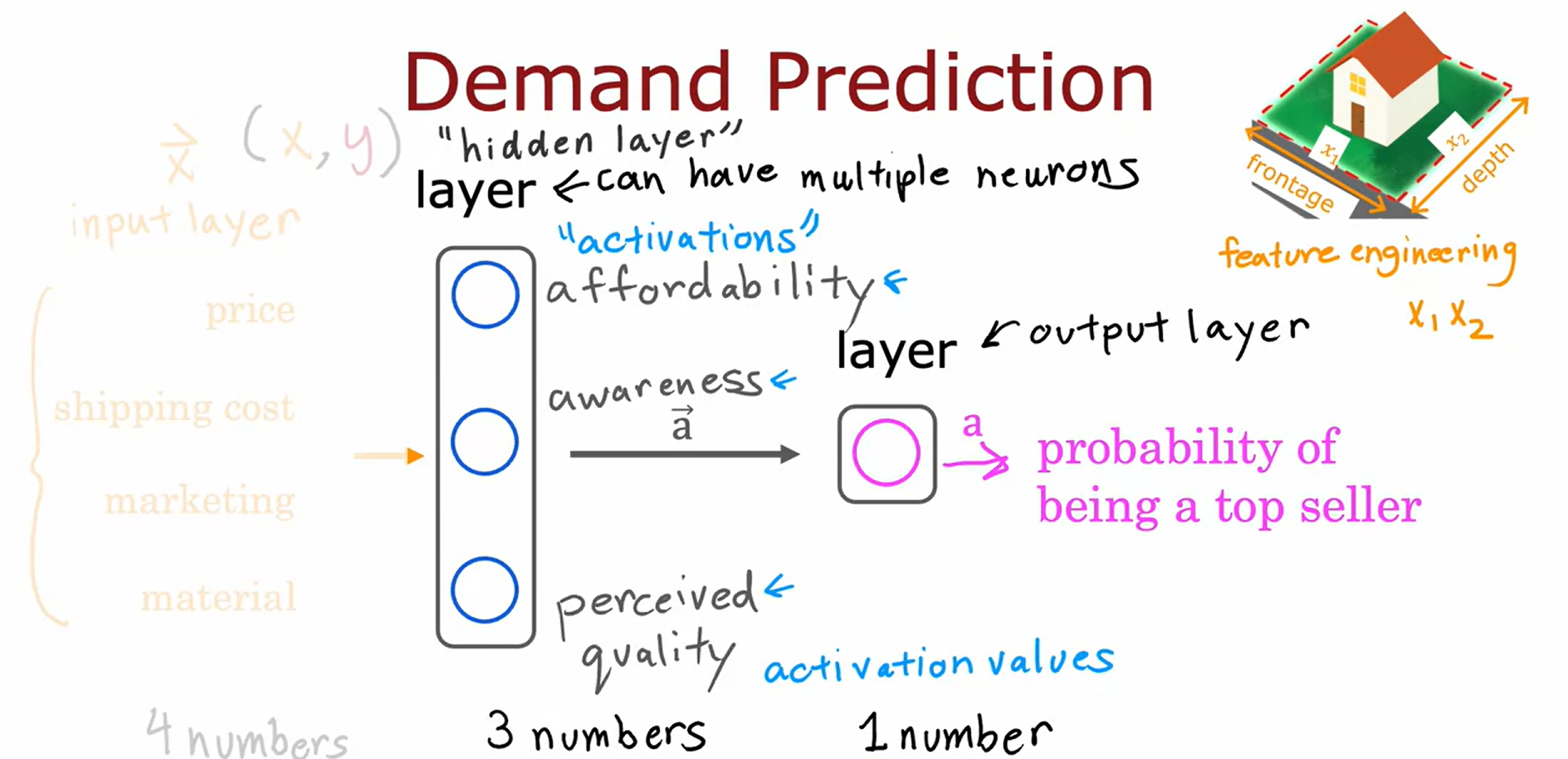
price, shipping cost 등 본래의 feature를 사용하는 대신 이를 조합해 affordability, awareness와 같은 feature를 사용하는 것이 최종 output을 구하는데 더 나은 방법이 된다. 이는 이전 시간에 공부했던 feature engineering이며, 이전 시간에 feature engineering을 수동으로 계산했던 것과 다르게 neural network는 feature engineering을 수동으로 할 필요 없이 스스로 feature를 학습하고 problem을 해결한다.
따라서 실제로 neural network를 훈련시킬 때는 affordability같은 다른 feature가 무엇인지 명시적으로 결정할 필요없으며, 이는 neural network가 스스로 학습한다.
hidden layer가 두 개 이상 있는 예시를 살펴보자.
아래와 같이 hidden layer가 몇개이고 hidden layer안에 neuron이 몇개인지에 대한 것은 neural network architecture의 문제이다.

먼저 왼쪽을 살펴보면 2개의 hidden layer를 가지고 있다.
중요한 점은 neuron의 개수와 activation의 개수는 일치한다는 것이다.
(하나의 뉴런이 하나의 activation을 출력하므로)
hidden layer에 neuron이 3개 있으면 3개의 activation으로 구성된 vector가 출력되며,
이 3개의 숫자를 두번째 hidden layer에 입력할 수 있다.
2번째 hidden layer에선 neuron이 2개이므로 2개의 activation으로 구성된 vector가 출력된다.
오른쪽도 hidden layer가 3개 이상으로 구성되어 있다는 점을 제외하곤 왼쪽과 같다.
일부 문헌에서는 여러 layer로 구성된 이러한 유형의 neural network를 "mutilayer perceptron(다층 퍼셉트론)"이라고 부른다.
Example: Recognizing Images
neural network를 computer vision에 어떻게 적용할 수 있을까?
아래와 같이 사진을 입력받아 사진 속 인물의 신원을 출력하는 neural network를 훈련시켜 얼굴 인식 애플리케이션을 개발한다고 가정해보자

해당 이미지의 크기는 1000x1000px이며 이는 pixel intensity(픽셀 강도)의 1000x1000 matrix라고도 한다.
(pixel 값은 0~255 사이의 값중 하나이다.)
이러한 pixel을 하나의 column vector로 표현하면 100만($1000^2$) pixel intensity의 vector가 생성된다.
(파란색 화살표를 따라 vector가 생성된다)
즉, 100만 pixel의 feature vector를 input으로 받아서 그림 속 인물의 신원을 출력하는 neural network를 훈련 시킬 수 있어야한다.
이를 위해 neural network는 아래와 같이 구성한다.
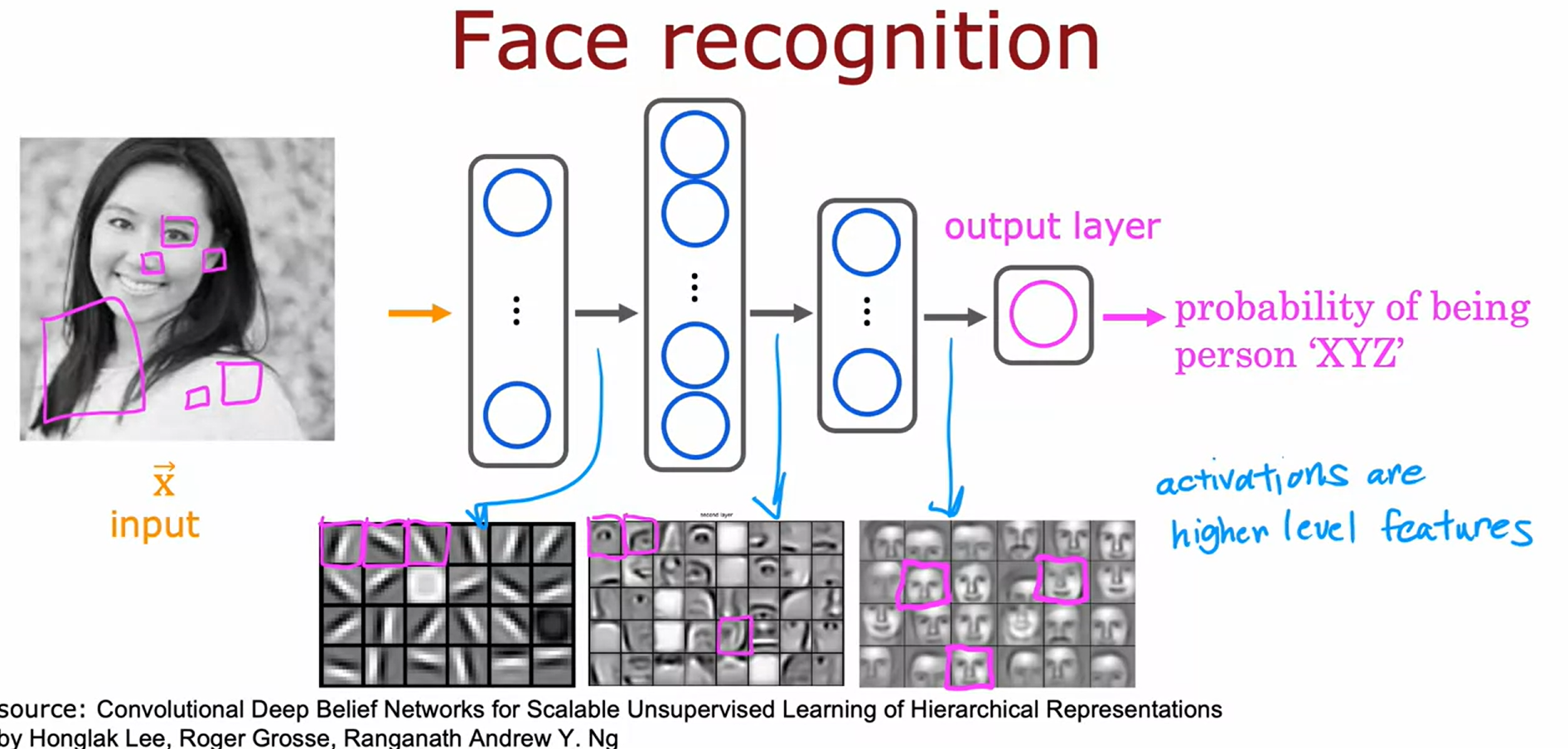
첫번째 hidden layer에서는 일부 특징을 추출하고, 출력값은 두번째 hidden layer의 input으로 들어가게 된다. 이와 같은 과정을 반복하면 output layer에서 최종적인 확률을 추정해낸다.
수많은 얼굴 이미지를 대상으로 training 하는 neural network를 살펴보고, 해당 hidden layer가 어떤 것에 대한 정보를 담고있는지를 시각화하여 계산을 시도해볼 수 있다.
1번째 hidden layer의 neuron은 낮은 수직선이나, 가장자리와 같은 방향을 가리키는 작은 "선"을 찾는 식이며
2번째 hidden layer는 얼굴의 일부를 찾기 위해 많은 선들을 그룹화하는 방법을 학습한다.(눈의 유무, 코끝 등등)
3번째 hidden layer는 얼굴의 여러 부분을 모아 더 큰 얼굴 모양의 유무를 감지하며, 사진 속 얼굴이 서로 다른 얼굴 모양과 얼마나 일치하는지를 감지하여 인물의 identity를 판단한다.
neural network는 여러 hidden layer에서 이러한 feature를 혼자서 학습할 수 있다.
예를들어 첫번째 layer에서 선을, 두번째 layer에서는 얼굴 부분을, 세번째 layer에서는 완전한 얼굴 모양을 찾으라고 한 사람은 아무도없으며, neural network가 data를 통해 이 모든 것을 스스로 알아낸다.

주의 해야할 점은 해당 시각화에서는 각 hidden layer에 따라 비교적 작은 window(확대된 사진)에서 더 큰 window로 나아가고 있다는 점으로, 위와 같이 작게 표시된 activation들은 아래처럼 hidden layer에 따라 다른 사이즈의 영역들을 가지고 있다는 점이다.(activation의 scaling을 맞춰서 위처럼 표현한 것 뿐이다.)

이번에는 다른 dataset으로 훈련시켜보자.

동일한 learning algorithm으로 자동차 탐지를 요청하면 경계선 -> 자동차 부품 -> 자동차 형태 감지의 순으로 학습을 시도한다.
이처럼 neural network는 서로 다른 데이터를 입력하는 것만으로도 매우 다른 feature를 감지하는 방법을 자동으로 학습해서 training 대상을 예측한다.
Neural network model
위에서 진행한 demand prediction 예제를 가지고 와서 neural network layer가 어떻게 작동하는지를 이해해보자.

3개의 neuron으로 구성된 hidden layer에 4개의 input feature를 설정한 다음 하나의 neuron(single neuron)이 있는 output layer로 출력을 보내는 형식이다.
hidden layer를 확대해서 계산과정을 살펴보자

hidden layer는 4개의 숫자를 input으로 받고, 4개의 숫자 모두 3개의 뉴런에 각각 input으로 들어간다.
또한, 하나의 neuron마다 하나의 logistic regression unit을 구현하고 있으며, 각기 다른 w와 b를 파라미터로 가진다.
첫번째 hidden unit이라는 것을 나타내기 위해서 $\vec{w}_1,b_1$처럼 아래 첨자를 붙인다.
해당 unit이 하는 일은 activation value $a$를 출력하는 것이다.
logistic regression에 따라서 activation value가 계산되고, activation에도 첫번째 뉴런이라는 것을 나타내기 위해서 $a_1$으로 아래첨자를 붙인다.
첫번째 neuron의 activation은 affordability(경제성)이었으므로 0.3이라는 값은 이 제품이 매우 저렴할 확률이 0.3%라는 것을 의미한다.
나머지도 2번째 뉴런, 3번째 뉴런임을 나타내기 위해 각 파라미터와 activation value에 아래 첨자를 붙인다.
위와 같이 각각의 neuron마다 개별적인 parameter들이 존재하며, 개별적으로 activation value를 계산한다는 점을 헷갈리지 않게 해라
이 예제에서 3개의 뉴런은 0.3, 0.7, 0.2를 출력하고, 이 세 개의 activation value로 구성된 vector를 $\vec{a}$로 나타낸다. 이후 $\vec{a}$는 output layer의 input으로 들어갈 것이다.
여러 layer로 구성된 neural network를 구축할 때 서로 다른 숫자를 지정하여 indexing하는 것은 유용하다.
즉, 아래와 같이 위 첨자를 이용해서 layer를 indexing할 것이다.
일반적으로 input layer를 layer 0, 그 다음의 hidden layer를 neural network의 layer 1이라고 하며, 그 다음의 layer(output layer)를 layer2라고 한다.

예를 들어, 위의 사진의 계산식은 layer 1에 관한 것이므로 $\vec{w}_1^{[1]}$과 같이 나타낸다.
또한, activation에도 위 첨자를 붙여 나타낸다.
이처럼 layer에 따라 위 첨자로 indexing한 것은 해당 layer와 관련된 quantity(수량)을 나타낸다.
예를 들어, $\vec{w}_1^{[1]}$면 layer 1에 대한 quantity를 의미하며,
$\vec{w}_1^{[2]}$면 layer 2에 대한 quantity를 의미한다.
다른 계층의 경우에도 마찬가지이다.
이제 layer 2의 계산을 확대해보자.

방금 계산한 activation vector가 layer 2의 input으로 전달되었다. output layer에는 neuron이 하나뿐이므로 위와 같이 하나의 sigmoid함수만으로 나타낸다. 하나의 neuron만을 가지므로 하나의 activation value를 가지며 vector가 아닌 scalar로 표현된다.
또한, layer 2의 quantity라는 것을 나타내기 위해 activation value와 파라미터에 [2]라는 위첨자가 붙은 것을 확인할 수 있다.
여기서 중요한 점은 input의 위첨자는 [2]가 아닌 [1]이라는 것이다.(이는 input이 layer 1의 activation value이기 때문이다.)
이제 마지막 단계를 확인해보자.

threshold를 0.5로 설정하고 이용하여 output layer의 activation value가 0.5이상이라면 1로, 아니라면 0이 될 것이라고 prediction을 만들 수 있다. 이를 통해 category(또는 class)를 분류해내는 것이 가능하다.
- More complex neural networks
이제 조금 더 복잡한 neural networks를 살펴보자.

해당 neural networks에서는 input layer를 제외하고 4개의 layer가 있다.
layer 0은 input layer, layer 1, 2, 3은 hidden layer고, layer 4는 output layer이다.
일반적으로 neural network에 4개의 layer가 있다고 하면 hidden layer와 output layer만 포함되고 input layer는 빼고 계산한다. 즉, 이 neural network는 일반적인 방식으로는 4개의 layer로 구성된 network이다.
layer 3를 확대해서 해당 layer의 계산을 살펴보겠다.

앞서 살펴본 것과 마찬가지로, 각 neuron(unit이라고도 한다)과 layer에 따라 첨자를 붙였으며, activation value에도 첨자를 붙여 layer3와 관련된 activaton라는 것을 나타내고 있음을 보여준다.
또한, 각 neuron마다 개별적으로 연산을 수행하고 있다.
layer 3에 input으로 들어온 값은 layer 2의 activation이기 때문에 input의 위 첨자는 `[2]`인것도 확인할 수 있다.
#Quiz

알맞은 것을 고르는 것이었다.
기억할만한 점은 input이 여러개일 때는 single number가 아닌 vector로 전달되어야한다는 점이다.
- Notation

즉 위와 같은 방법 식으로 나타낸다.
위첨자([$l$]는 layer, 아래 첨자([$j$])는 neuron(즉, 각 단위(unit)를 뜻함)에 대한 indexing이며, input으로는 이전 layer의 output이 들어가므로 $[l-1]$의 첨자를 가지고 있음을 확인할 수 있다.
함수 $g$(sigmoid function)는 activation value를 출력하기 때문에 activation function(활성화 함수)라고도 불린다.

또한 activation에 대한 표기법을 동일하게 나타내기 위해서 위와 같이 input vector x를 $\vec{a}^{[0]}$로 나타낸다.
이를 이용해 위의 방정식의 input으로 input vector x를 $\vec{a}^{[0]}$로 적용시킬 수 있다.
Inference: making predictions (forward propagation(순방향전파))
손으로 쓴 숫자를 0과 1로 구분하는 예를 사용해보자.
해당 예제는 binary classification으로 표현할 수 있다.

각 이미지는 8x8 pixel intensity로 구성된 matrix이다.
(255는 밝은 흰색 pixel을, 0은 검은색 pixel을 나타낸다)
이 64개의 input feature을 고려해서 두개의 hidden layer가 있는 신경망을 사용해보겠다.

25개의 unit을 가진 layer는 25개의 activation value를,
15개의 unit을 가진 layer는 15개의 activaton value를 가진다.
앞서 설펴봤던 표기법으로 이를 나타냈다.
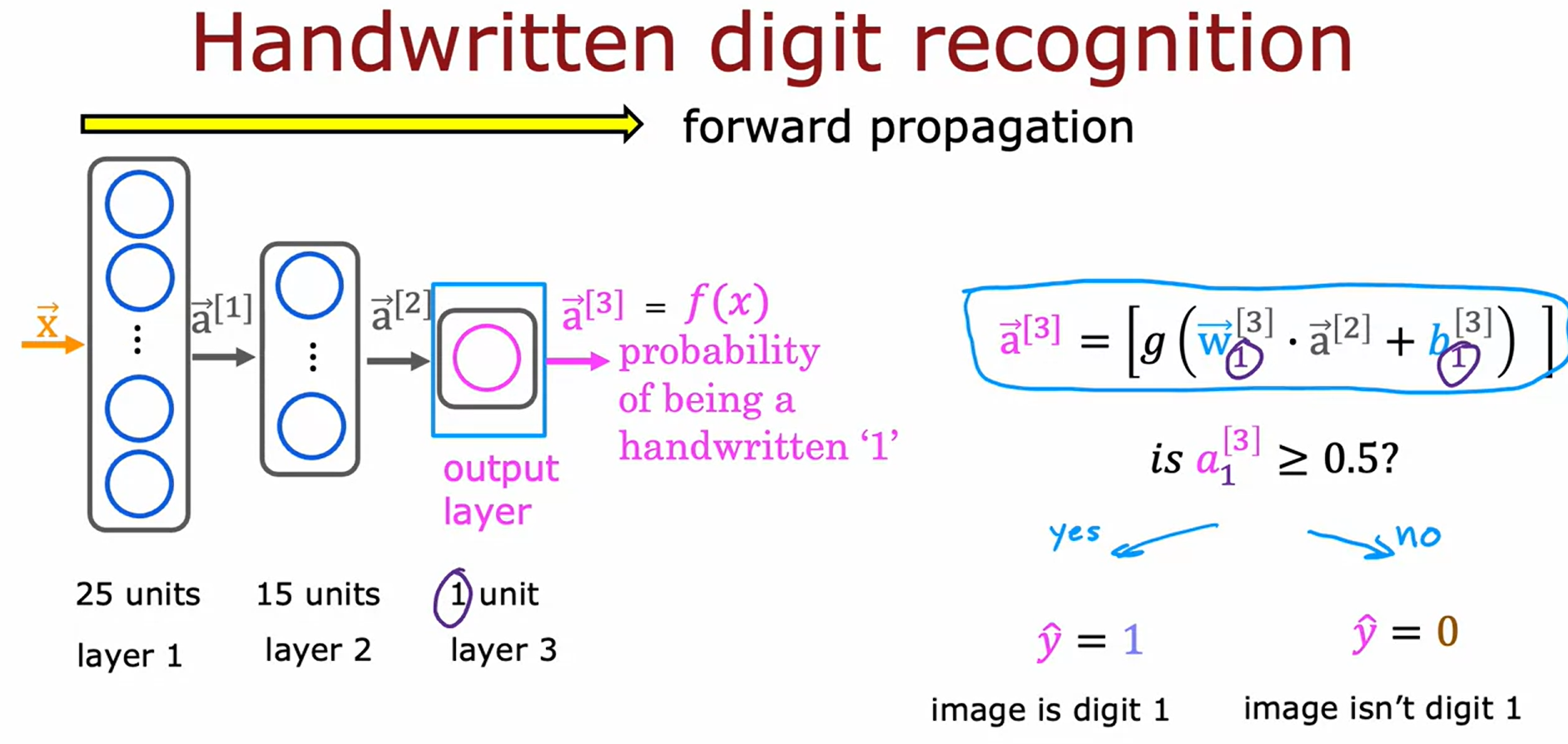
이후의 step은 threshold를 사용하여 $\vec{a}^{[3]}$를 계산하는 것이다.
unit(neuron)이 하나뿐이니 $\vec{a}^{[3]}$는 scalr값으로 나타난다. => $a_1^{[3]}$
neural network의 출력값이기도 한 $\vec{a}^{[3]}$는 $f(x)$로 쓸 수도 있다.($a=g(z)$이기 때문에, logistic regression이나 linear regression의 출력을 나타내기 위해서는 f(x)를 사용했었다.)
해당 계산은 왼쪽에서 오른쪽으로 진행되므로 x부터 시작해서 $\vec{a}^{[1]}$, $\vec{a}^{[2]}$. $\vec{a}^{[3]}$를 차례로 계산한다.
즉, neuron의 activation을 순방향(순서대로)으로 전파하기 때문에 forward propagation(순방향 전파)라고도 한다.
처음엔 hidden unit이 많다가 output layer에 가까워질수록 hidden unit의 수가 줄어드는데, 이는 neural network architecture를 선택할 때 자주 사용되는 꽤나 일반적인 선택이다.


